Abstract
Background: The aneurysm refers to the increase in arterial diameter in a localised position and this is characterised by the non-parallelism of the arterial wall. Despite prediction models trying to anticipate the onset of an aneurysm, the limits of their accuracy are often reached. This is due to the poor definition of the factors favouring the development of the aneurysm. In order to take into account this complex process, this study proposes a fuzzy system in the analysis of the effect of each factor.
Methods: As the variability of the diameter of the aorta is a function of several uncertain and imprecise factors, this study deals with data relating to a population of 100 patients diagnosed at the level of the service of the UFAS Setif Hospital in Algeria. This study is limited to the effect of age, which is related to the diameter of the abdominal aorta diagnosed. A fuzzy inference analysis system is proposed. As the system is very complex and in an uncertain environment, its fuzzy logic analysis compensates this uncertainty.
Results: Once the system is established from the actual values recorded, it becomes possible to introduce the input variables randomly to automatically read the result at the output with maximum precision.
Conclusions: In order to avoid the risk of rupture, it is necessary to diagnose the aneurysm according to the patient’s age. The introduction of the variables relating to the patient at the entry of the system allows clinicians to have a precise idea about the aneurysm. Note that the majority of cases are diagnosed accidentally in the absence of a screening program.
Key Points
2. Factors affecting abdominal aneurysm development are often difficult to detect by prediction models.
3. The authors present a study in favour of a fuzzy interference analysis system, which can be used to counteract uncertainty and provide accurate results in a highly complex system.
INTRODUCTION
The abdominal aortic aneurysm is often silent and has no visible symptoms.1 It is necessary to take care of an abdominal aneurysm in time because it is at risk of bursting. A high percentage of aneurysm cases that are not treated in time have their chance of recovery diminished. This makes it necessary to detect aneurysms prematurely, as long as detection is rapid and reliable.2 The problem with abdominal aortic aneurysms is to be able to act before they rupture by identifying them and defining when to treat them as they progress. A screening program is needed to prevent the development of the aortic aneurysm, and therefore to intervene before it is too late.3
As a preventive measure, monitoring and follow-up programs for abdominal aneurysms have been put in place. The scheduled time between two successive examinations is determined by the diameter of the aorta. When the diameter is large, the time between examinations is shortened. The goal is to monitor the critical limit of this diameter so that it does not reach 50 cm.4
Since the aortic aneurysm is characterised by the absence of symptoms, to be able to screen a population in a wide range it is essential to have a selection plan, taking into account the risk factors. The problem is that risk factors are distinguished by their uncertainty, complexity, and imprecision. This study deals with the analysis of these factors by artificial intelligence (AI) techniques. The principles of fuzzy inference are proposed in this analysis. A fuzzy system is established with input variables that represent the factors involved in the aortic aneurysm, a database that links inputs to output, and an output of the system that expresses the risk of occurrence of the aneurysm. As each variable is considered fuzzy, and therefore uncertain, the fuzzy analysis compensates for these uncertainties, and the result will be as precise as possible.
RISK FACTOR
Several factors are involved in the development of the aneurysm. However, some factors are much more relevant. These include smoking, high blood pressure, age, dyslipidemia, sex, atherosclerosis, and familial predispositions.5 This study is limited to the age factor only. It is noted that this factor in itself remains a function of several other auxiliary factors such as weight, comorbidity, physiology, and intrinsic metabolism. From there emerges the complexity of the system. Also noted is that this disease is a function of geographical distribution.6
AGE
In addition to the race factor, the age factor is a direct function of the diameter of the abdominal aorta.7 This is interpreted by the fact that with advanced age, other pathologies are associated such as diabetes, hyperlipidemia, or high blood pressure.8 By considering the age factor as a fuzzy variable, the associated factors are then taken into account in an indirect way. In general, with advanced age, the risk of an aneurysm is much higher.9 This prompted the Society for Vascular Surgery (SVS) to issue recommendations to systematically screen male patients from the age of 65 regardless of the associated factors. This remains valid for females as well. When the genetic factor is taken into account in males, this age is reduced to 55 years.10
METHOD
The study sample includes 100 diagnosed patients. Measurements of the diameter of the abdominal aorta were performed by CT scan. This diameter was correlated with the age factor. This factor is also a function of other parameters such as smoking, blood pressure, and sex, as well as family predispositions. As these variables are imprecise and complex, the authors consider them to be fuzzy variables. These factors constitute the input variables to the analysis system. An output variable expresses the diameter of the corresponding aneurysm, and therefore its risk of possible bursting. A database is built connecting the input variables to the output variable (Figure 1). This base is established from the actual values recorded. The general form of a rule that connects inputs to output is of the form: ‘If… then’. Mathematically, the resulting output variable is a function of the input variables: output = F (A,G,P,F), where A is age, S is sex, P is arterial pressure, and F is family history.
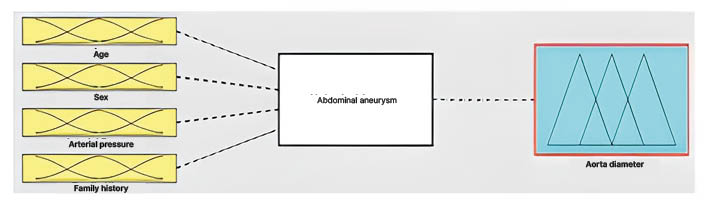
Figure 1: System bloc diagram.
One of the techniques of AI is analysis by the principles of fuzzy inference. Like human reasoning, this technique compensates the uncertainties and inaccuracies to extract a clear decision.11
Fuzzy Analysis
Given the intrinsic nature of biological systems which are characterised by their uncertainty, problems of predictive control of these models can be modelled as dynamic programming problems. The information is distributed and parallel. Several factors influence the system.12
Sometimes classical mathematical methods are inapplicable to analyse complex phenomena. The principles of fuzzy logic applied to this study are adequate. In classical binary logic, an element either belongs to a set, or does not belong. The fuzzy analysis is based on the partial membership of a set.13 This way of thinking has the advantage of being flexible, simple, and compatible in the analysis of complex, imprecise, and uncertain systems. The authors express the variables in degrees of truth on the membership function. Like human reasoning, they express variables in linguistic terms. For example, the variable ‘age’, presented in classical logic by the numeric value in years, is suppressed by a linguistic value such as ‘young’, ‘adult’, or ‘old’. Belonging to the function is not binary, but belonging to the youth or adult group, for example, is.
All of the variables are considered fuzzy. Therefore, the first phase is their fuzzification. This operation allows their conversion from digital to symbolic. The variables are then expressed in linguistic language.
Fuzzification of Input Variables
Each variable must be fuzzified; this consists of their conversion from numeric to linguistic expression in human language.
The age variable
The age of the patients is fuzzified into three fuzzy triangular-type membership functions: young (0–30 years); adult (25–60 years); old: (55–100 years). There is the creation of overlap zones between two neighbouring intervals. This allows compensation for the uncertainty in the allocation of age ranges. This method is applied to all the variables to fuzzifier (Figure 2). In the same way, the other factors are fuzzified.
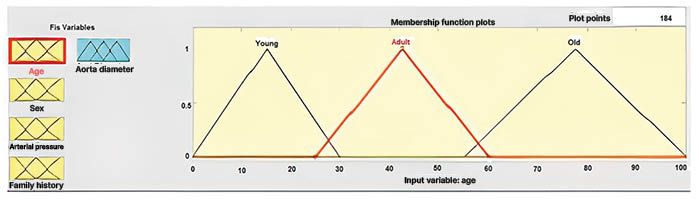
Figure 2: Fuzzification of the age variable.
The sex variable
The sex variable is not fuzzified. This variable is expressed in numeric terms: male (1) and female (2).
The arterial pressure variable
The arterial pressure variable is fuzzified into three fuzzy triangular-type membership functions:
- Low (0-2; 120/80 mmHg);
- Medium (1-3; 120–129/< 80 mmHg);
- High (2-4; >130–139 mmHg systolic or 80–89 mmHg ‘diastolic’).
These numerical assignments translate the degree of blood pressure.
The family history variable
The family history variable is fuzzified into three fuzzy triangular-type membership functions. According to the family history, the effect of this factor and its influence is approximately estimated as absence (0–2), risky (1–3), or certain (2–4).
This numerical attribution expresses the probability of the effect of family history.
Output variable
People diagnosed positive according to their aorta diameter are represented by numeric values from 2.5–6 cm. The diameter of the aorta is fuzzified into three membership functions according to their recorded diameter. Again, overlapping intervals are created to compensate the imprecision of the assignment of linguistic variables: normal (2-4), risky (3-5), or severe (4-6). Matlab 2016a (MathWorks, Portola Valley, California) is used for data processing.
RESULT
The basis of the rules is established from the actual recorded values. The uncertainties of the variables age and sex, blood pressure, and the effect of family history variable are compensated by the fuzzification process. Each case mapped to the output variable, which is also fuzzified.
When the base of the rules includes all of the possible combinations, it suffices to introduce any variables at the input to read the result at the output. The result read at digital output is compared to the fuzzification function of the diameter of the aorta to be situated in linguistic terms. (Figure 3).
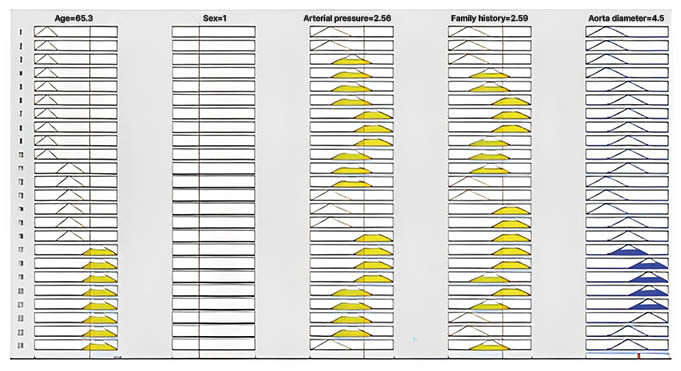
Figure 3: Example of application.
CONCLUSION
The factors involved in the development of the aneurysm are multiple and complex to analyse by conventional methods. This study proposes a model based on AI techniques, in particular the principles of fuzzy inference.
By the fuzzification process, the numeric variables are converted into linguistic variables in human language. It comes close to the rough reasoning that comes out with the most exact result possible. The inaccuracies are then compensated. Age as a determining factor in the appearance of the aneurysm, and is also a function of other associated factors that this study takes into account. The database established from 100 diagnosed patients makes it possible to encompass a large number of possible rule combinations that map the input variables to the diameter of the aorta recorded. When the system is complete, it is possible to read the result at the output from the random values at the input.
The output value is calculated from the aggregation of all the rules.
As there is no screening program available everywhere, this tool can be an aid in the diagnosis and prevention of abdominal aneurysm.